在矩阵理论中，旋转矩阵是一种特殊的正交矩阵，用于描述空间中的旋转运动，在矩阵运算中，左乘和右乘是两种基本的矩阵乘法运算方式，本文将详细探讨旋转矩阵左乘和右乘的区别,帮助读者更好地理解这两种运算方式在旋转矩阵中的应用。

旋转矩阵概述

旋转矩阵是一种特殊的正交矩阵，用于描述空间中的旋转运动，在三维空间中，一个旋转运动可以通过绕任意轴旋转任意角度来描述，旋转矩阵可以用来表示这种旋转运动，使得我们可以将旋转运动表示为矩阵运算，旋转矩阵具有一些特殊的性质，如正交性、行列式为1等。

矩阵左乘与右乘的基本概念

在矩阵理论中，左乘和右乘是两种基本的矩阵乘法运算方式，左乘表示将一个矩阵放在左边，右乘表示将一个矩阵放在右边，这两种乘法方式在运算结果上有很大的区别，左乘和右乘的结果取决于矩阵的维度和性质,以及参与运算的矩阵之间的关系。

旋转矩阵左乘与右乘的区别

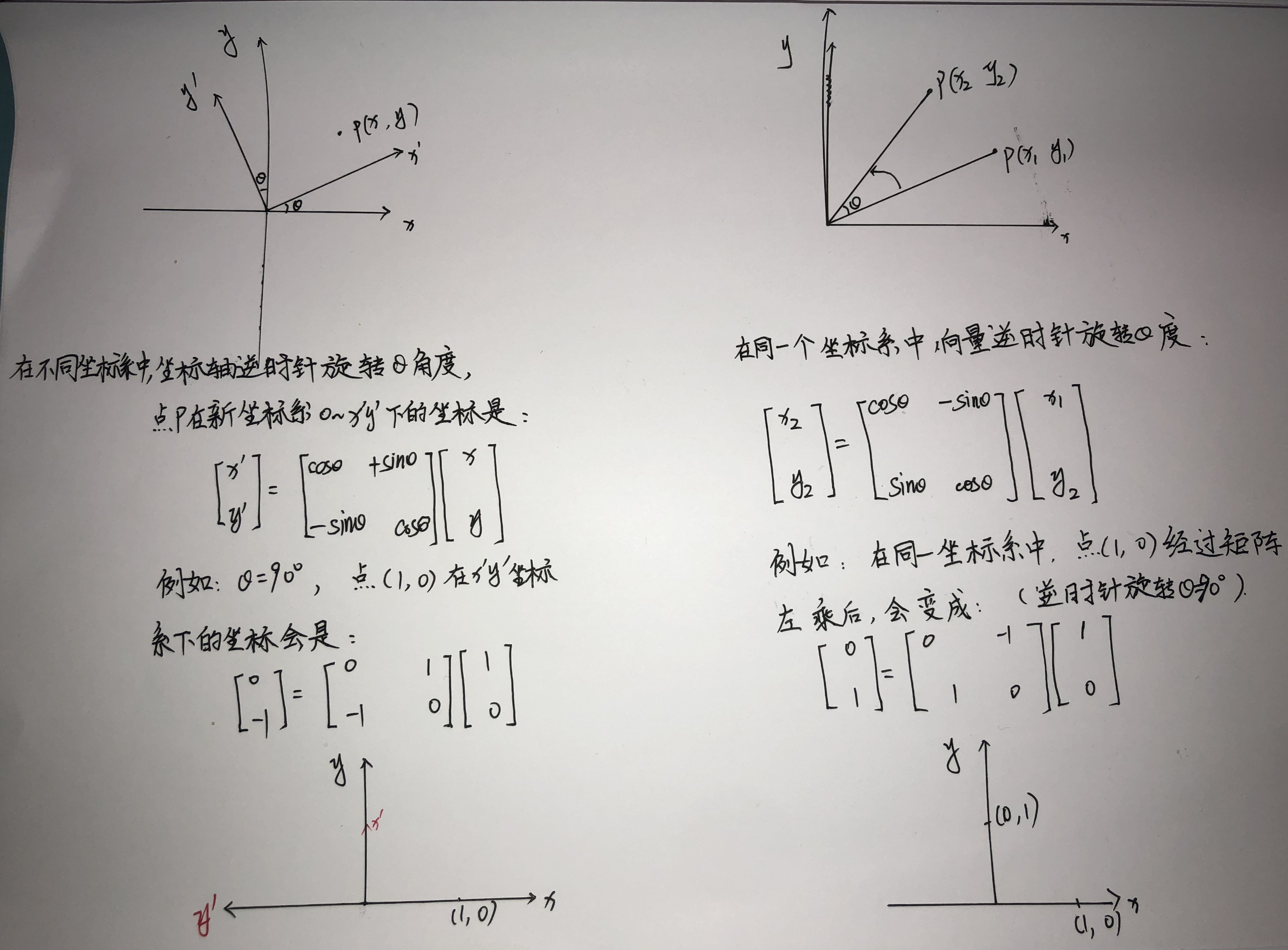
1. 运算结果：旋转矩阵左乘和右乘的运算结果不同，左乘一个旋转矩阵通常用于表示对一个向量进行旋转，而右乘一个旋转矩阵则用于表示旋转矩阵自身的变换，这是因为左乘和右乘在矩阵乘法中的运算顺序不同,导致结果也不同。
2. 几何意义：在几何空间中，左乘一个旋转矩阵可以表示将一个向量按照旋转矩阵描述的旋转运动进行旋转，而右乘一个旋转矩阵则可以表示将旋转矩阵本身进行变换,即将一个旋转运动转换为另一个旋转运动。
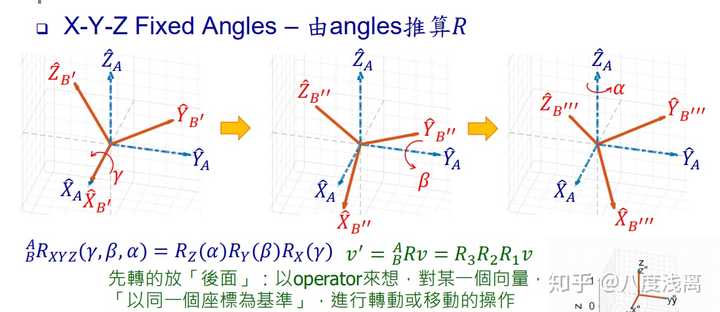
3. 性质与特性：由于左乘和右乘的运算结果不同，因此它们在性质上也存在差异，连续左乘多个旋转矩阵仍然是一个旋转矩阵，而连续右乘多个旋转矩阵则不一定是一个旋转矩阵，左乘和右乘在行列式、迹、特征值等矩阵性质上也有所不同。

应用实例

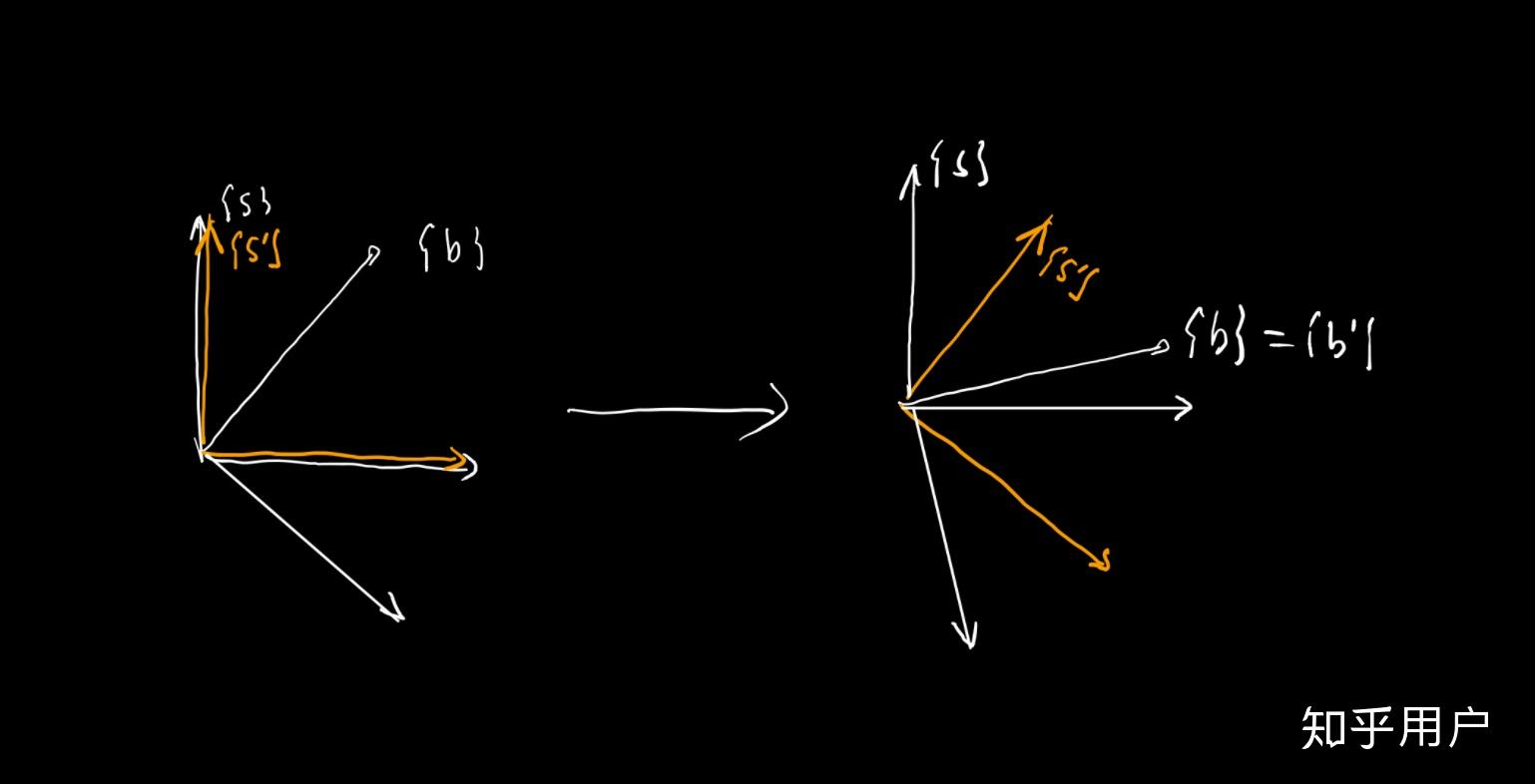
1. 机器人学：在机器人学中，旋转矩阵常用于表示机器人的姿态，左乘一个旋转矩阵可以用于表示机器人末端执行器的姿态变换,而右乘一个旋转矩阵则用于表示机器人本体坐标系之间的转换。
2. 计算机视觉：在计算机视觉中，旋转矩阵用于表示图像之间的变换关系，左乘一个旋转矩阵可以用于图像矫正和校准,而右乘一个旋转矩阵则用于描述图像之间的相对关系。
3. 物理学：在物理学中，旋转矩阵用于描述刚体的运动，左乘一个旋转矩阵可以用于表示刚体的旋转运动,而右乘一个旋转矩阵则用于描述不同坐标系之间的转换。

本文详细探讨了旋转矩阵左乘和右乘的区别，包括运算结果、几何意义、性质与特性以及应用实例，通过了解这些区别，我们可以更好地理解旋转矩阵在各个领域中的应用，并更好地利用旋转矩阵进行空间变换和姿态描述，在实际应用中，我们需要根据具体情况选择合适的乘法方式,并充分利用旋转矩阵的性质和特性进行运算和分析。

随着科技的不断进步和应用的不断拓展，旋转矩阵的应用将会更加广泛，对于左乘和右乘的研究也将更加深入，未来研究方向可以包括：研究更高效的算法进行旋转矩阵的左乘和右乘运算；探索新的应用领域，如虚拟现实、增强现实、无人驾驶等；研究旋转矩阵与其他数学工具的结合，如四元数、齐次坐标等,以更好地进行空间变换和姿态描述。

参考文献

[此处插入参考文献]

致谢

感谢各位专家和学者对本文的指导和支持，感谢同行专家的宝贵意见和建议，也要感谢读者们的关注和支持,希望本文能对读者有所帮助和启发。