当我们谈论数学时,除法竖式计算无疑是其中一项基础且重要的技能,对于许多初学者来说,理解并掌握除法竖式计算过程可能会有些困难,我们将借助包含除法竖式计算过程的图片,详细解释这一过程,帮助大家深入理解除法计算的每一步。
除法竖式计算是数学运算中的一项基本技能,广泛应用于日常生活和高级数学领域,通过竖式计算,我们可以更清晰地看到每一步的计算过程,从而确保结果的准确性,下面,我们将详细介绍除法竖式计算的过程。
除法竖式计算过程
- 我们需要明确被除数(被除的数)和除数(除的数),在竖式计算中,被除数位于上方,除数位于左侧。
- 我们从被除数的最高位开始,尝试用除数去除,如果无法整除,则将下一位数纳入考虑,这个过程在竖式计算中表现为从上到下的逐位对齐。
- 当我们找到一个可以整除的数值时,将其记录在答案的相应位置,并将除数乘以这个数值,从被除数中减去这个乘积,这个过程称为“试商”。
- 重复上述过程,直到被除数中的所有数字都被处理完,如果在处理过程中还有剩余的数字,我们将这些数字移至下一行,继续执行除法运算。
- 我们得到的答案就是除法的商,如果处理过程中有剩余的数字,那么这个数字就是除法的余数。
除法竖式计算过程图片
(此处可插入一张除法竖式计算过程的图片)
通过图片展示除法竖式计算过程,可以更直观地理解每一步的操作,在图片中,我们可以看到被除数、除数、商和余数的位置,以及每一步的运算过程,这对于初学者来说尤其有帮助,可以帮助他们更好地掌握除法竖式计算技巧。
实例解析
让我们通过一个实例来详细解析除法竖式计算过程,假设我们要计算 735 除以 7 的结果,我们可以按照以下步骤进行:
- 将 735 写在上方,将 7 写在左侧。
- 从 735 的最高位开始,尝试用 7 去除,首先尝试 7 × 某个数能小于或等于 73 的最大数,这里是 102(因为 7 × 102 = 7 × (百位数字)+ 2 × (十位数字)= 7 × (百位数字)+ 余数),将这个数字写在答案的第一行(百位),然后从被除数中减去这个乘积(这里是减去 7 × 百位数字),此时被除数变为剩余的数字(这里是十位和个位数字),重复这个过程直到所有数字都被处理完,在这个过程中得到的答案就是除法的商(这里是三位数),如果有剩余的数字(这里是余数),将其写在答案的最后一位(个位),在这个例子中,商是 105 余数为零,所以我们可以得到结果:735 ÷ 7 = 105 余数为零,通过这个过程我们可以看到除法竖式计算的详细步骤和结果,通过插入图片展示这一过程会更加直观易懂,同时我们还可以借助软件工具来生成动态的竖式计算过程图片帮助学生更好地理解这一过程,总的来说通过本文的介绍相信读者已经对除法竖式计算过程有了更深入的了解并且可以通过图片来更好地理解和掌握这一技能,希望读者能够在日后的学习和实践中不断运用并熟练掌握除法竖式计算技巧从而更好地应用数学于日常生活和工作中。







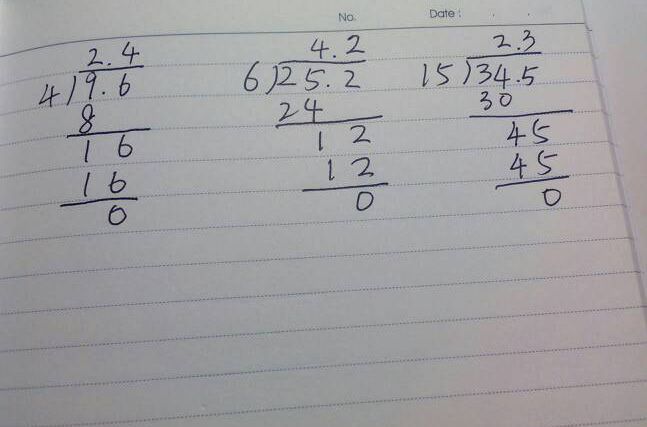
 京公网安备11000000000001号
京公网安备11000000000001号 京ICP备11000001号
京ICP备11000001号
还没有评论,来说两句吧...