在基础数学教育中,除法是一项至关重要的运算技能,特别是在涉及小数点的除法运算时,竖式计算图发挥着不可替代的作用,本文将详细介绍小数点除法竖式计算图的原理、步骤及应用,帮助读者更好地理解和掌握这一技能。
什么是小数点除法竖式计算图
小数点除法竖式计算图是一种用于解决小数点除法问题的直观方法,通过设立竖式计算图,我们可以系统地展示除法运算的每一步,从而帮助我们更好地理解并解决小数点除法问题,这种方法的优点在于其清晰、直观,有助于我们逐步解决问题,避免出错。
小数点除法竖式计算图的原理
小数点除法竖式计算图的原理基于除法的定义和性质,在竖式计算图中,我们将被除数和除数按照一定规则排列,然后通过逐步相减或相除的过程,得到商和余数,在这个过程中,我们需要特别注意小数点的位置,确保计算的准确性。
小数点除法竖式计算图的步骤
- 设定位置:将被除数和除数按照要求设定在竖式计算图中,确定小数点的位置。
- 从高位开始:从被除数的最高位开始,按照顺序逐位进行除法运算。
- 商的确定:根据每一步的运算结果,确定商的数值。
- 余数的处理:每一步运算后,处理产生的余数,将其与下一步的被除数一起参与运算。
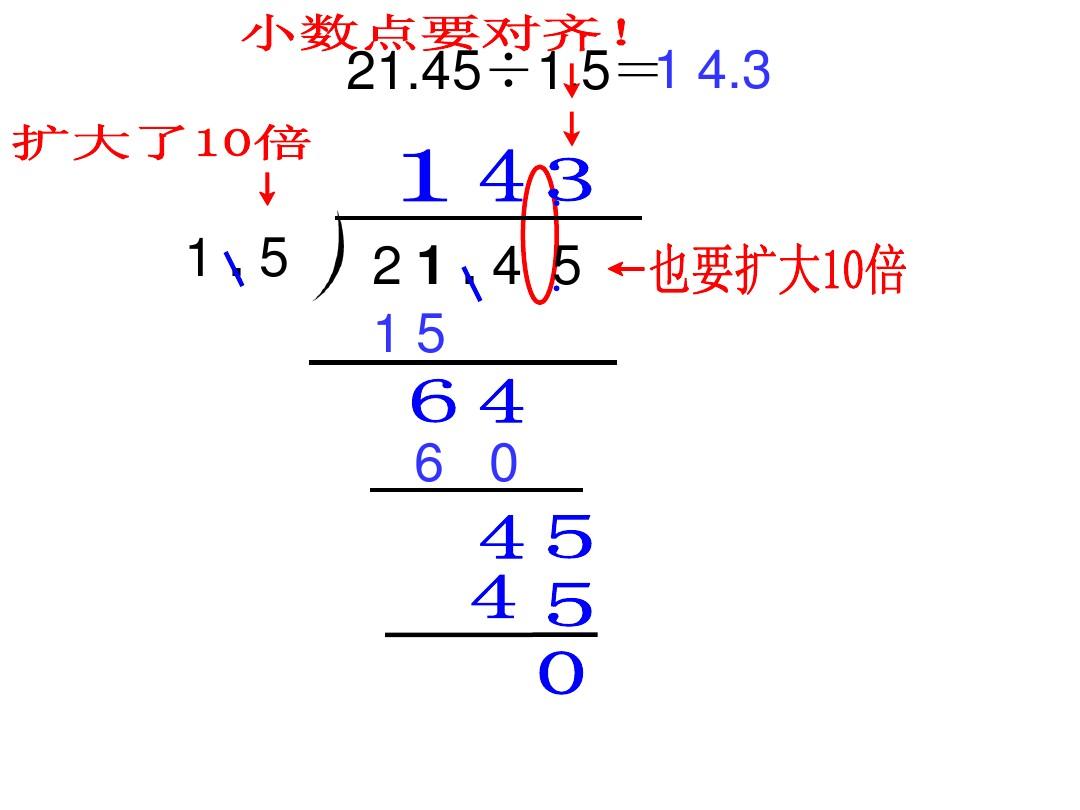
- 小数点的移动:在运算过程中,根据需要将小数点向右或向左移动,以保持计算的准确性。
小数点除法竖式计算图的应用
小数点除法竖式计算图广泛应用于日常生活和工业生产中,在商品定价、财务管理、科学研究等领域,我们经常需要处理涉及小数点的除法问题,通过掌握小数点除法竖式计算图,我们可以更快速、准确地解决这些问题,提高工作效率。
实例演示
为了更好地理解小数点除法竖式计算图的应用,下面以一个实例进行演示:
假设我们需要计算 13.2 ÷ 3 的结果,我们可以按照以下步骤进行:
步骤1:设定位置,将 13.2 作为被除数,3 作为除数,设定在竖式计算图中,确定小数点的位置。 步骤2:从高位开始,从被除数的最高位(即个位)开始运算,得到商为 4 余数为 1(即第一次运算后剩余的被除数),此时小数点位置不变。 步骤3:继续运算,将余数作为新的被除数(即 1),与下一步的除数(即 3)进行运算,得到商为 0 余数为 2(即第二次运算后剩余的被除数),此时小数点位置向右移动一位,将余数作为新的被除数(即 0.2),与下一步的除数(即 3)进行运算,得到商为 0 余数为 0(即第三次运算后剩余的被除数为零),此时小数点位置保持不变,最终得到的商为 4.4,我们可以得出结论:13.2 ÷ 3 = 4.4,通过竖式计算图的应用,我们可以清晰地展示每一步的运算过程,确保计算的准确性,这种方法也有助于我们更好地理解除法的原理和方法,在实际应用中,我们可以根据具体的问题选择合适的方法进行计算,无论是手动计算还是使用计算器辅助计算,掌握小数点除法竖式计算图都是非常重要的基础技能之一,七、结论通过本文的介绍和实例演示可以看出小数点除法竖式计算图是一种直观易懂的方法它有助于我们更好地理解和掌握小数点的除法问题通过设立竖式计算图我们可以清晰地展示每一步的运算过程从而确保计算的准确性同时这种方法也有助于我们更好地理解除法的原理和方法在日常生活中我们会经常遇到涉及小数点的除法问题因此掌握小数点除法竖式计算图是非常必要的通过不断练习和实践我们可以更加熟练地掌握这一技能从而提高工作效率和准确性在未来的学习和工作中我们将受益于对小数点除法竖式计算图的深入理解和应用总之小数点除法竖式计算图是数学学习和应用中的重要工具之一通过本文的介绍我们希望能够帮助读者更好地理解和掌握这一技能并在实际应用中发挥更大的作用

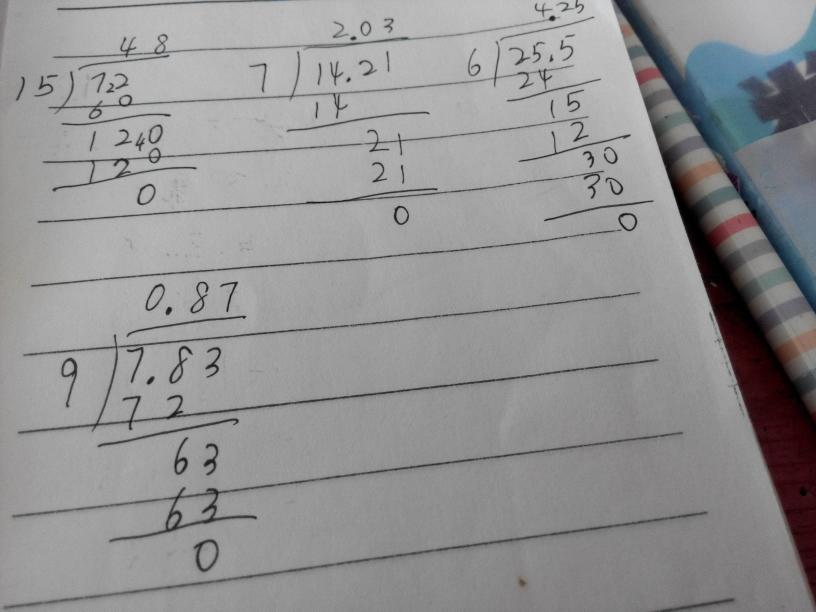




 京公网安备11000000000001号
京公网安备11000000000001号 京ICP备11000001号
京ICP备11000001号
还没有评论,来说两句吧...