除法竖式计算是数学运算中的基本方法之一,广泛应用于日常生活和各类科学计算,通过竖式计算,我们可以清晰地看到每个数在运算过程中的变化和作用,本文将详细解析除法竖式计算中每个数的含义,帮助读者更好地理解除法运算的本质。
除法竖式计算概述
除法竖式计算是从被除数开始,通过除号、除数、商和余数等元素的相互作用,得出最终结果的运算过程,在这个过程中,每个数都有其特定的含义和作用。
除法竖式计算中的每个数表示
- 被除数:需要被分割或分配的总数量,在竖式计算中,被除数通常位于竖式的上方,表示需要被除的数。
- 除数:用来分割或分配被除数的数,在竖式计算中,除数位于除号后面,表示每份的数量或标准。
- 商:除法运算的结果,表示被除数可以被除数整除的次数,在竖式计算中,商通常位于竖式的右侧,表示被除数按照除数分割的次数。
- 余数:除法运算后剩余的部分,在竖式计算中,余数位于竖式的下方,表示被除数按照除数分割后剩余的部分。
除法竖式计算的详细解析
以被除数为17,除数为3的除法竖式计算为例,我们可以按照以下步骤进行解析:
- 将被除数17写在竖式的上方。
- 将除数3写在除号后面。
- 从被除数的最高位开始,用除数去除被除数,17除以3得到商为5余2。
- 将商5写在竖式的右侧。
- 将余数2写在竖式的下方。
通过这个例子,我们可以看到被除数、除数、商和余数在竖式计算中的具体作用和含义。
除法竖式计算中的每个数都有其特定的含义和作用,通过理解这些数的含义,我们可以更好地理解除法运算的本质和过程,在实际应用中,掌握除法竖式计算方法对于提高数学运算能力和解决实际问题具有重要意义。
拓展与应用
除法竖式计算不仅应用于基本的数学运算,还广泛应用于各种领域,在财务管理中,我们可以通过除法竖式计算来计算单位数量的成本或收益;在物理学中,我们可以利用除法竖式计算来分析物理量的比例关系;在统计学中,除法竖式计算可以帮助我们计算平均值、比例等统计数据。
本文通过详细解析除法竖式计算中的每个数的含义,帮助读者更好地理解除法运算的本质,通过实例演示,我们了解了被除数、除数、商和余数在竖式计算中的具体作用和含义,掌握除法竖式计算方法对于提高数学运算能力和解决实际问题具有重要意义,希望本文能够帮助读者更好地掌握除法竖式计算方法,并将其应用于实际生活中。









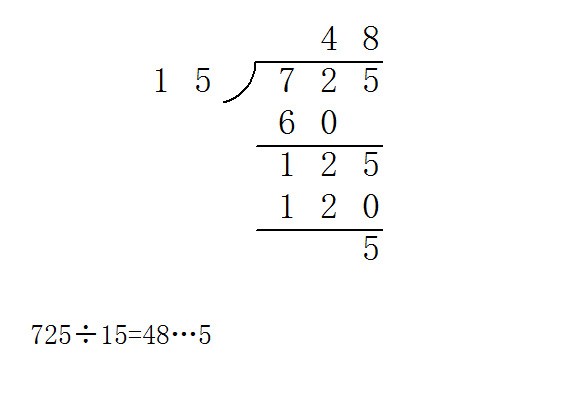
 京公网安备11000000000001号
京公网安备11000000000001号 京ICP备11000001号
京ICP备11000001号
还没有评论,来说两句吧...